We see microphones everywhere – musicians on stage, politicians at a podium, preachers at the pulpit, artists in recording studios. Everyone wants to sound louder and be heard clearly.
The job of a microphone is to convert sound waves into an electrical signal. Once the sound is converted to an electrical signal, we can amplify, modify, and record it.
Microphones detect sound with some type of movable element that vibrates in sympathy with the air pressure. The vibrations of the movable element are used create an electric current. The way they do this defines what type of microphone it is. In this article we will look in detail at the four main types of microphones: dynamic, electret, condenser, and ribbon.
Characteristics and Specifications
It is important to understand what the different microphone specifications mean, because it will allow you to select the right one for a given purpose.
- Sensitivity – This is the output voltage the microphone will deliver for a given sound pressure level (SPL), expressed as millivolts per Pascal (mV/Pa).
- Maximum SPL – This describes the maximum loudness (in dB) that a microphone can handle without damage or distortion. This is important to consider if the microphone will be used with loud instruments such as drums. An average level is about 100 dB, and a high SPL is 130 dB. Dynamic microphones can handle higher SPLs, whereas ribbon microphones are more sensitive and delicate.
- Frequency response – This is the range of frequencies a microphone can reproduce without attenuation, typically 50Hz to 15kHz. This range will vary depending on the orientation of the source to the microphone. Frequency response may improve at the low end if the microphone is close the sound source.
- Directivity – Microphones have different sensitivities depending on the position of the source relative to the microphone. some microphones are more sensitive from the front, others more sensitive on the sides.
- Impedance – This is the AC resistance of the microphone. The impedance of most microphones is around 50Ω to 200Ω. Dynamic microphones may be a bit higher at 600Ω. The input impedance of the amplification system should be higher than the microphone to prevent loading.
Types of Microphones
Dynamic Microphones
Dynamic microphones work in much the same way as a loudspeaker, but in reverse. There is diaphragm attached to a coil that is inside a strong magnetic field. As the sound pressure moves the diaphragm and coil in and out of the field, a voltage is generated. These microphones are rugged and able to deal with strong SPL levels, such as concert venues. They are less sensitive than their condenser and ribbon cousins but offer good value for money. Shown below is a typical dynamic microphone.

Electret Microphones
Electret condenser microphones have a diaphragm and backplate that are electrically charged. will vary their relative distance to each other as sound moves the diaphragm. When sound waves cause the diaphragm to vibrate, a changing voltage is created. This requires a very high impedance FET transistor to buffer and amplify the audio signal. This means an external source of voltage is required.
The thin, lightweight diaphragm makes electrets very sensitive compared to dynamic microphones, with good frequency response. They can be made very small, making them easy to fit within many different products.
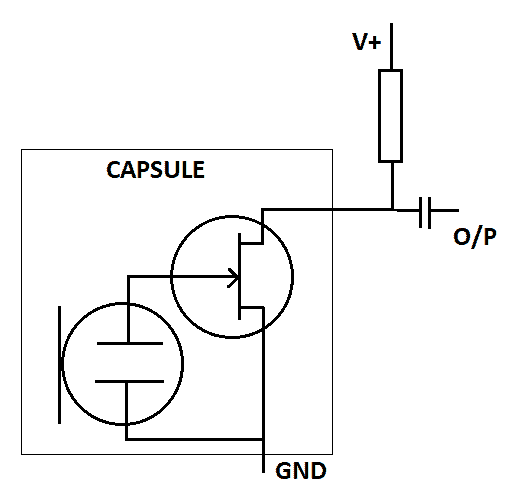
Shown below at left is a typical electret microphone with a matchstick for scale. The schematic shows the inside of the capsule with the FET and the external load resistor (typically about 10k).
 |  |
Condenser Microphones
As the name implies, condenser microphones use a condenser to detect sound. Condensers are made up of a solid backplate and a closely spaced metalized diaphragm. As the diaphragm vibrates, its distance from the backplate changes, causing the capacitance to change.
A voltage (either from an internal battery or from the cable) is applied across the two plates, and as the capacitance changes, a voltage is produced. Condenser microphones have good frequency responses and are better for handling high frequencies. Shown below is a studio-quality condenser microphone with an anti-pop screen.

Ribbon Microphones
Ribbon microphones are used in the studio for recording voices and a broad range of instruments. They soften the sound and impart warmth to recorded material. They have the most natural response of all microphones. Inside, the ribbon is suspended in a magnetic field, with electrical contacts at each end of the ribbon. As the ribbon vibrates in the magnetic field, a voltage is produced. Shown below is a studio ribbon microphone.

Connecting Microphones
Professional quality microphones are usually connected to other equipment with an XLR cable. Most mixing boards will have an adjustable pre-amplifier for each microphone channel to match the volume to other instruments.
Clearly, you should choose a microphone according to your purpose. Cost and ruggedness are usually the most important considerations. Many microphones come with special features, and there are even wireless microphones available. Some situations call for anti-shock support systems. Many sound recording engineers also use anti-pop shields to filter out vocal pops and wind noises.
Hope this article helps you pick the best amplifier for your needs! Feel free to leave a comment below if you have any questions.


It was very informative to know that dynamic microphones are made to be used at concert venues because it has a strong SPL level. Me and my friend are planning on hosting a gig next month. We’re going to be inviting a lot of local bands and guests, so we want to make sure everything from the sound system to the logistics are spot-on. We’ll surely find a reputable company who can rent us the necessary equipment.