Ohm’s law, Joule’s law, and an understanding of power and energy are among the most fundamental and important foundations for understanding electricity and electronics.
Energy is an object’s ability to do work. Even a block of wood on your table possesses energy. It has kinetic energy as it can do work as it falls, and it possesses chemical energy as it can do work to heat if you set fire to it. Energy is expressed in Joules. When you allow energy to do work, such as releasing chemical energy stored in a battery into a resistor, this work is expressed as power.
Power is the rate of doing work. One Watt spent in one second is one Joule. So for instance, a car needs more power to travel at 100km/h compared to 50km/h. When you have spent power over a period of time, or purchased prepaid electricity to use, or have a certain size of battery that is charged, you have Watt-hours. Say, you put 1000 W/h into your prepaid electricity meter, you could use it up by running a 1kW heater for 1 hour or a 100W light for 10 hours. The same amount of energy gets used, just at different rates because a thousand (1000) Watts is equal to one (1) kW.
On the other hand, a Joule is the unit of energy used by the International Standard of Units (SI). It is defined as the amount of work done on a body by one Newton of force that moves the body over a distance of one meter.
Ohm’s Law
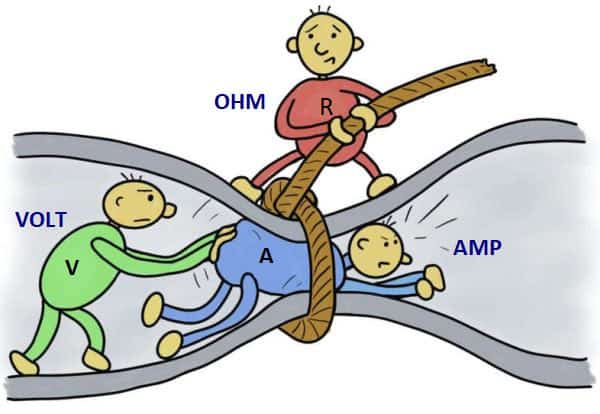
This cartoon perfectly sums up Ohm’s law. Here we have Mr. Volt trying to push Mr. Amp through the conductor, but Mr. Ohm is doing his best to restrict Mr. Amp. With a bit of imagination, you can see that the harder (more pressure) Mr. Volt exerts, the more Mr. Amp will get through. On the other hand, the more Mr. Ohm pulls on the rope (resists), the less Mr. Amp will get through. These three live in perfect balance and proportion to each other. The rule that keeps them in balance is Ohm’s law.
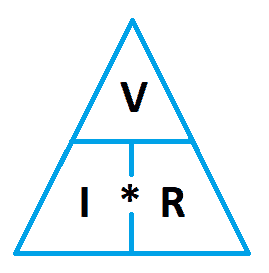
Putting it more formally, we can use the triangle above. Learn this by heart, as this is an easy way to remember all the formulas. Simply point your finger over the unit you want to find, and the remaining two are what you will calculate with. For example, if you want to find V, cover V with your finger, and you are left with I*R. This means that V=I*R. Likewise, if you wanted to find I, cover I with your finger, and you are left with V/R. This means that I = V/R.
Note that we use I for Amp and not A because A is universally used to denote area.
For example, if I have a 9V battery and I connect a 1k resistor across it, how much current will flow through it?
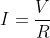
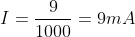
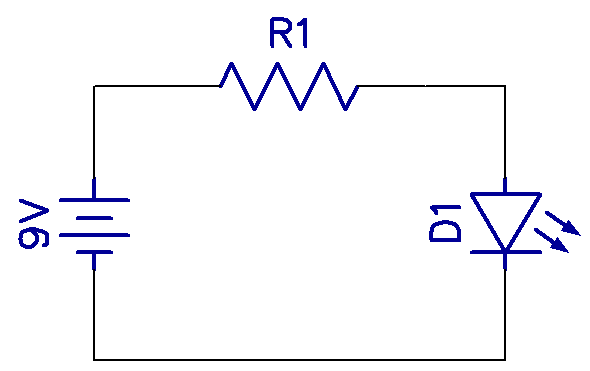
Say I have a 9V battery, and I want to light up a LED. You can’t just connect the battery to the LED as it will draw as much current as the battery can provide and will burn out. We need to limit the current in the LED to a safe value with a resistor. First, I need to know how much voltage the LED needs, and secondly, how much current I will allow in the LED—typically 20mA. The voltage that an LED will set up across it is fairly constant and will depend on the color. A red LED is typically 2.3V.
So we now have 9V on one end and 2.3V on the other end of R1, meaning we have to get rid of 9-2.3 = 6.7V. This is the voltage we would see if we measured across the two ends of resistor R1, and the current through it is 20mA. Given that R=V/I = 6.7/20*10-3 = 335Ω. This means that a 330Ω resistor would be fine.
Let’s say we didn’t know any of the above, and we just grabbed a 1k resistor and put it in series with the LED, then we took our trusty multimeter and measured the voltage across the LED and found it to be 2.7V. That means the voltage across the resistor must be 9-2.7 = 6.3V. So now, what current is flowing through the LED? Using the formula I=V/R again, we find 6.3/1000 = 6.3mA.
Now, let’s say you had a very long extension cord, and you were running a heater or a big spotlight, and you knew the current in the wire was 15A, and the wire resistance was 1Ω. How much voltage would you lose along the wire? Using the formula V=I*R, we find that you’re losing 15*1 = 15V, which is quite a lot.
Power and Joule’s Law
Power is the term used to describe the rate of doing work or work over time. This means that a 100W lightbulb is running much hotter than a 1W lightbulb, and we can sense the work being done by the heat generated. Power is directly linked to Ohm’s by Joule’s law, which says that the heat produced in resistance is proportional to the square of the current flowing through it over a given time.
We can express this as P=V*I and because V=I*R, we get P = I*I*R or P=I2R.
In the same way P=V2/R. Like Ohm’s law, this is summarized in a triangle like this:
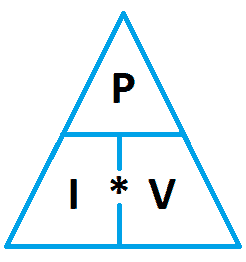
All of these terms are people’s names and so we always use capital letters. These units can get very large and can be expressed as kV or MΩ or very small such as mV or uA. Note that the unit is mA and not MA.
Energy
Energy is defined as “the property that must be transferred to an object to perform work on, or to heat, the object. Energy is a conserved quantity; the law of energy conservation states that energy can be converted in form but not created or destroyed. The SI unit of energy is the joule, which is the energy transferred to an object by the work of moving it a distance of one meter against a force of one newton”. And 1W is 1 Joule spent in 1 second.
In other words, power is the rate at which we change electric energy into some other kind of energy, usually heat but could also be motion, as in a motor. When you talk on your cell phone, you convert chemical energy from the battery into electromagnetic energy to transmit your voice. But a fair bit of the energy always gets converted into heat due to imperfections in the transmitter amplifier and other circuits.
Going back to our previous example of the extension cord, let’s say we could not measure the current in the extension wire, but we knew the heater was 2kW, and it was a 230V heater. Now we know that P=V*I, so I must be P/V, and so, 2000/230 = 8.7A. If we were able to measure the voltage at the end as, say, 200V. We would then know the cable’s resistance to be V/I = (230-200)/8.7 = 3.4Ω.
Energy also tells us about the rate by which work can be done. If I buy a battery that says 200mA/h, it tells me I can draw 200mA for 1 hour from it or 20mA for 19 hours. In my house, I have pre-paid electricity, which I purchase in kWh. If my stove uses 4kW and I purchased 40kWh, I could bake cookies for 10 hours.
Although these laws and calculations may seem boring, remember that these are vital to grasp and to be able to use them in the world of electronics. Thanks for reading and feel free to leave a comment below if you have any questions!







This is the best article I have seen explaining this principle and I really like the cartoon.
Best example of the V/I/R relationship I’ve seen. Thanks for the article.
” It has kinetic energy as it can do work as it falls, ”
Right idea, wrong word. A block of wood sitting on a desk has POTENTINAL Energy. When the block falls the Potential Energy is converted to Kinetic Energy. Same is true for the Chemical Energy – It is Potential Chemical Energy. It becomes Kinetic Energy when the temperature of the block is raised to a point of combustion.
Barry