Capacitance is defined as the ratio of the change in the electric charge of a system to the corresponding change in its electric potential. This term is used for capacitors, electrical components designed to store electric charge. In this article, we will investigate the concept of capacitance and how it applies to everyday electronics.
History
The concept of capacitance was introduced with the creation of an electric component called the capacitor. It was discovered in 1975 by Ewald Georg von Kleist. He discovered that electric charges coming from an electrostatic machine could be stored and released after a short period of time. The device that he used to do this became known as a Leyden Jar.
Capacitance is measured in Farads and is expressed in terms of the ratio of the change in the electric charge of a system to the corresponding change in its electric potential.
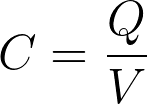
Energy Stored in a Capacitor
The energy stored in a capacitor is equivalent to the area under the graph of the voltage measured across a capacitor against the total charge of the capacitor.
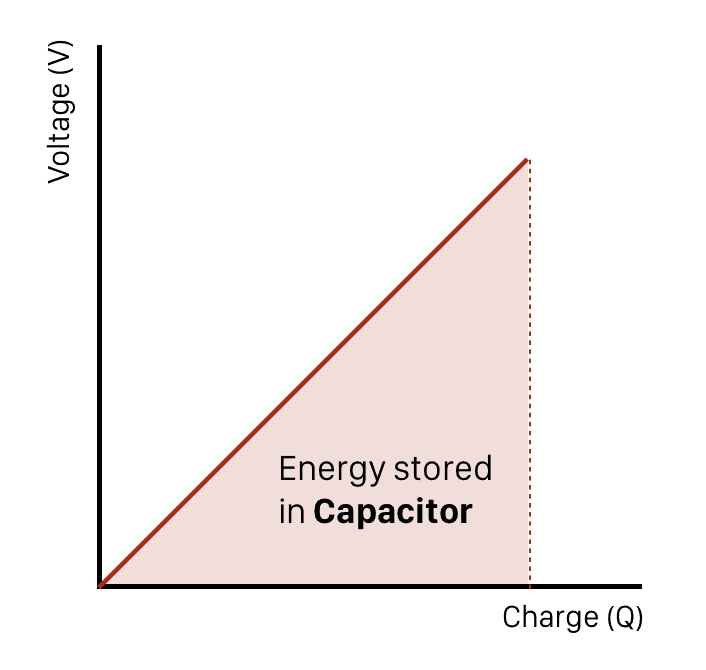
This can be expressed as:
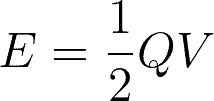
Which is equivalent to:
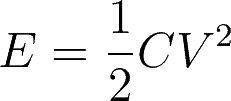
Capacitors in Series & Parallel
You may remember these circuit configurations from our article on resistance. However, the equations we use to describe the total capacitance in a series and parallel circuits are flipped.
Capacitors in Series
For capacitors in series, we use the following equation to calculate the total capacitance.
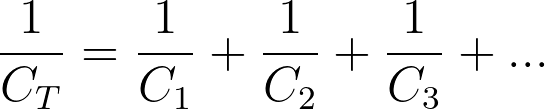
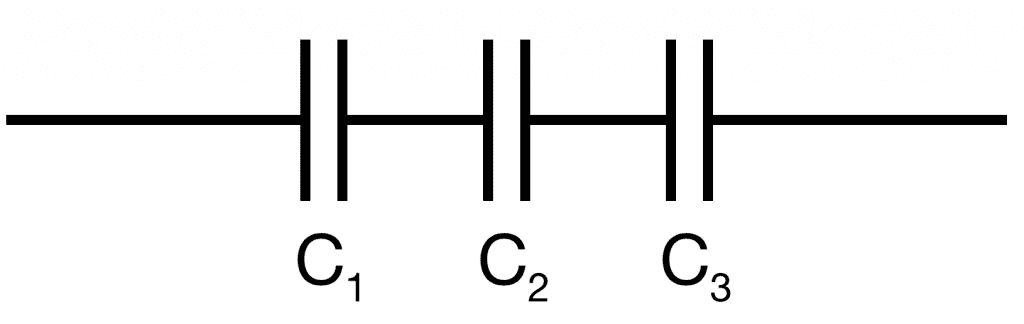
Here is a circuit schematic for three capacitors connected in series:
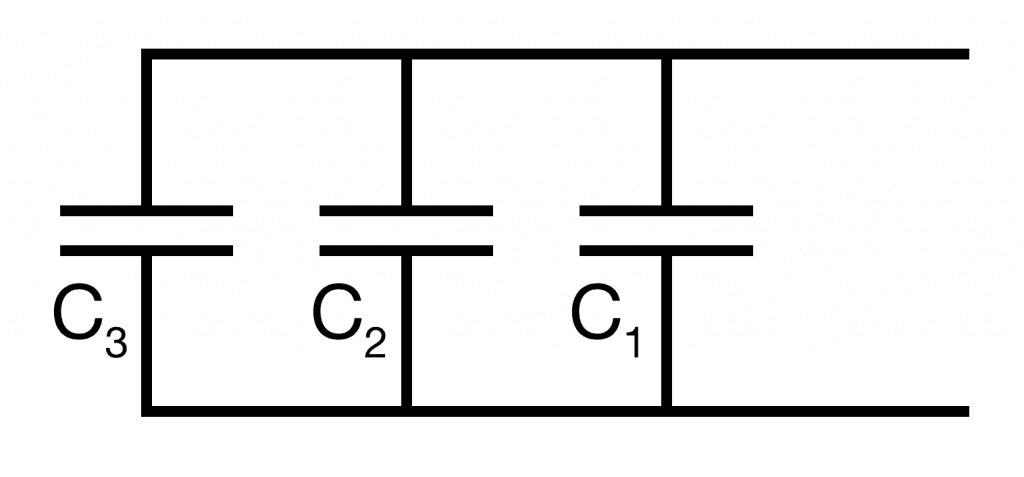
Capacitors in Parallel
For capacitors in a parallel configuration, we using the following equation to calculate the total capacitance.

This the schematic for three capacitors connected in parallel:
Time Constant
The concept of the time constant is important to understand because it determines how long a capacitor takes to charge and discharge.
The time constant of a capacitor can be calculated using T = R x C.
A capacitor can only be charged or discharged when paired with a load (a resistor)—which is the value of R (in Ohms) in the time constant equation. At the same time, C is the capacitance of the capacitor in Farads.
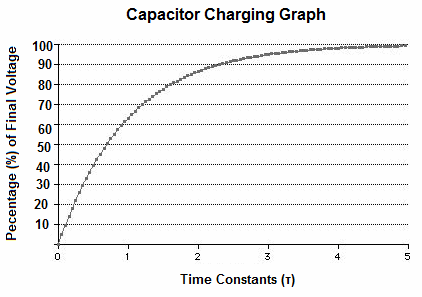
In one time constant, the capacitor reaches 63% of the total voltage when charging. In 5 time constants, a capacitor can be said to be fully charged or discharged.
Charging a Capacitor
This graph models the voltage across a charging capacitor with respect to the time constant.
This equation is used to model a charging capacitor:
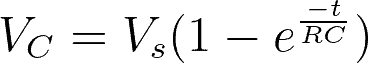
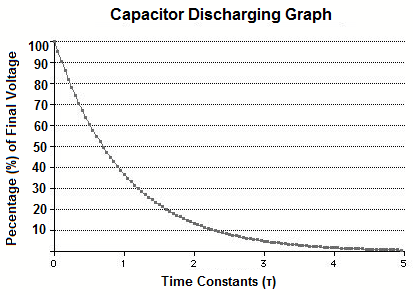
Discharging a Capacitor
This graph models the voltage across a discharging capacitor with respect to the time constant.
This equation is used to model a discharging capacitor:
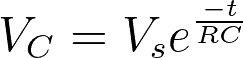
Capacitors and AC Current
Throughout this article, we have been discussing how DC current interacts with a capacitor. With DC current, a charge will continue to flow until the capacitor is fully charged. At that point, no current will flow. This has the effect of blocking DC current flow through a capacitor.
On the other hand, AC oscillates in different directions, resulting in a continuous switch between charging and discharging a capacitor: a widely used phenomenon in the communications industry. Thus, AC current is said to be able to pass through a capacitor.
That’s it for the basics of capacitance! Please feel free to ask any questions in the comments section below.






Check your date for discovery of the Leyden jar. You show 1975 in your article, date should be 1745.
Leyden Jar is around 1745 and officially presented 1746
In each of the five Time Constants the charge increases by 63% of the remaining voltage each time. For instance, if 10v is applied, after the 1st TC the voltage will be 6.3v.
After the 2nd TC the voltage rises by (10v – 6.3v) x 63% =2.33v. Plus 6.3v gives 8.63v.
After the 3rd TC the voltage rises by (10v – 8.63v) x 63% = 0.86v. Plus 8.63v gives 9.49v.
After the 4th TC the voltage rises by (10v – 9.49v) x 63% = 0.32v. Plus 9.49v gives 9.81v.
After the 5th TC the voltage rises by (10v – 9.81v) x 63% = 0.119v. Plus 9.81v gives 9.929v.
After the 6th 7th 8th TCs the voltage is even closer to 10v, but never gets there. This is why 5 x TC is considered close enough to call the capacitor “fully charged”.