In this tutorial, you will learn the fundamentals of neural networks and deep learning – the intuition behind artificial neurons, the standard perceptron model, and the implementation of the model in Python. This will be the first article in a pair of neural networks and deep learning tutorials.

PCBWay Ad

Biological Neurons

Figure 1: Neuron

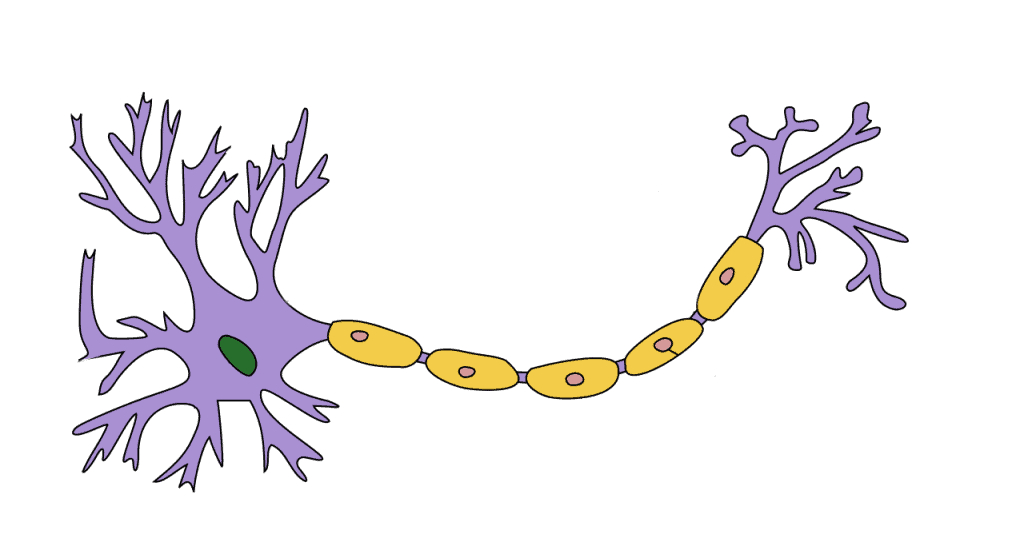
Neurons are interconnected nerve cells that process and transmit electrochemical signals in the brain. There are approximately 100 billion of them inside of us, with each neuron connected to about 10,000 other neurons.

A neuron works when a dendrite receives information (in the form of electrochemical energy) from other neurons. It then modulates the signal and passes the information to the cell nucleus (the green blob in Figure 1) for processing. Then, the nucleus sends the output data through the axon (the yellow bridge) to the axon output terminals or synapse. The synapses send the data to the next neurons.

Each neuron consists of multiple dendrites, which means there are multiple inputs as well. If the sum of these electrical inputs exceeds a certain threshold, the nucleus will activate the neuron, passing the signal to other neurons, which may trigger again.

Note that neurons only activate if the total signal received exceeds a certain threshold. It’s either no, we will not send a signal, or yes, we will. Our entire brain works according to the system of chain reactions of these elementary processing units.

This is what artificial neural networks aim to replicate. Today, though still far from modeling the brain’s entire complexity, ANNs are powerful enough to do simple human tasks such as image processing and formulating predictions based on past knowledge.

Artificial Neurons: Perceptron

Figure 2: Perceptron

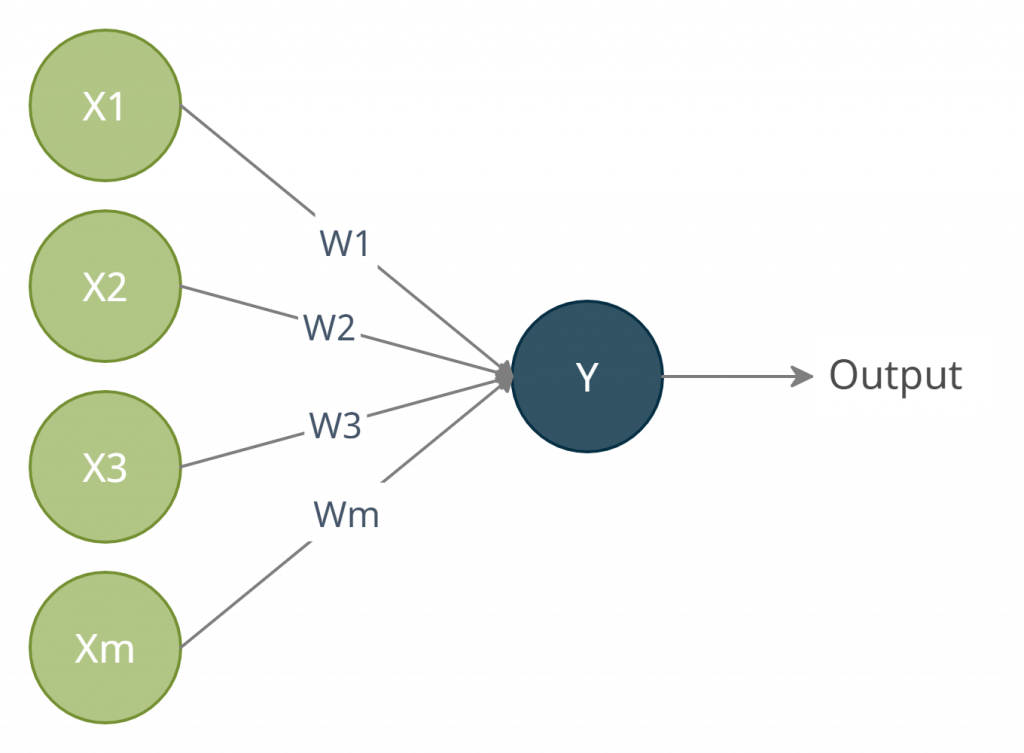
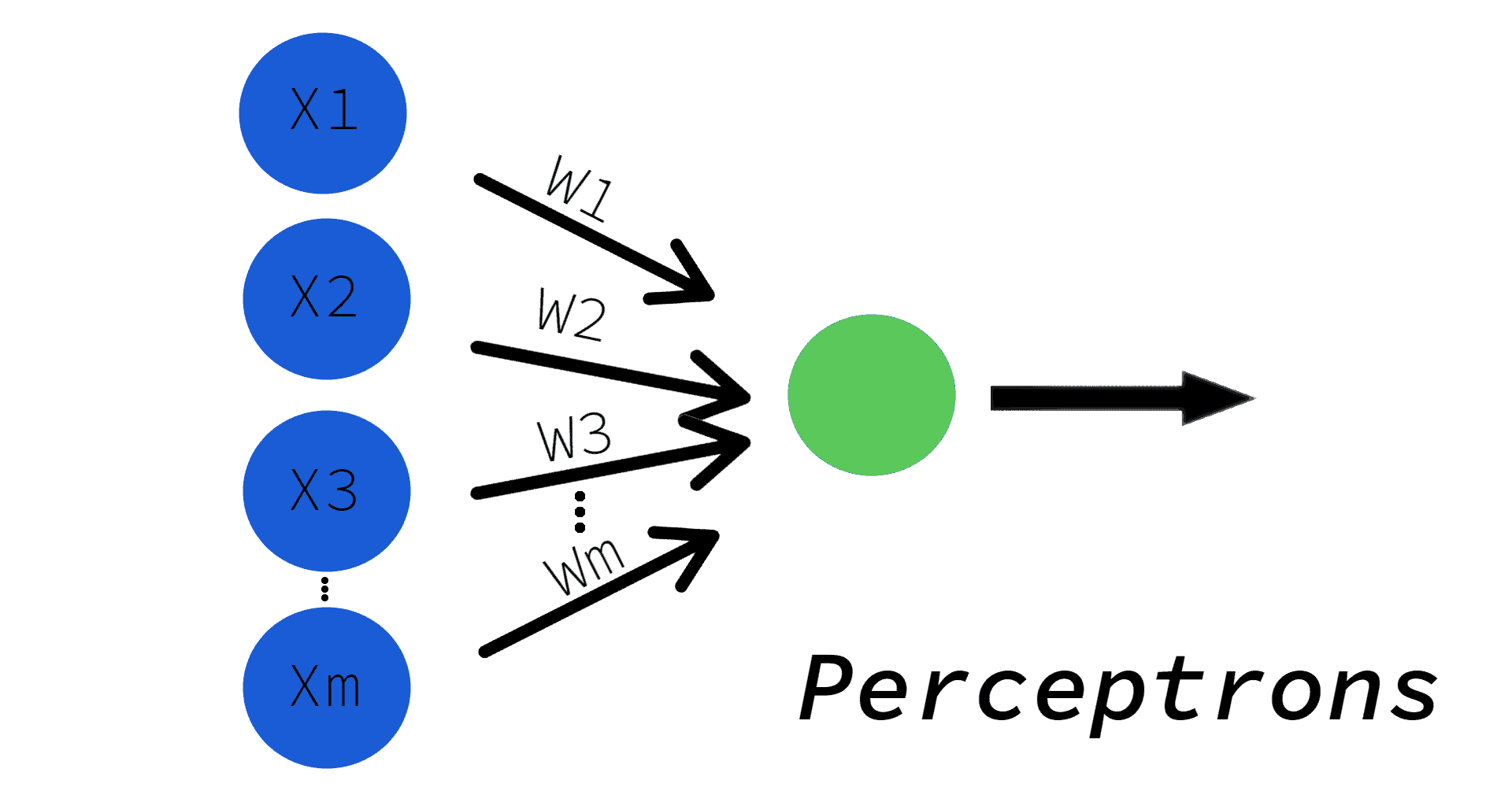
A perceptron is an artificial neuron. Instead of electrochemical signals, data is represented as numerical values. These input values, normally labeled as X (see Figure 2), are multiplied by weights (W) and then added to represent the input values’ total strength. If this weighted sum exceeds the threshold, the perceptron will trigger sending a signal.

You can call a perceptron a single-layer neural network.

Standard Equation

Equation 1 shows the mathematical characterization of the output Y of a perceptron.

Equation 1

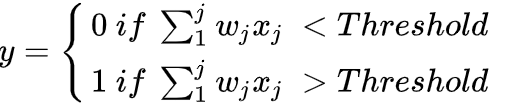
If the summation of all weighted values is less than the threshold constant, y equals zero. Otherwise, y equals one.

We can simplify the equation further with Equation 2.

Equation 2

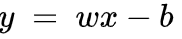
This form also makes it easier to code. If the product of wx is greater than b (bias), y will be positive and is therefore true. If the product is less than b, y will be negative and thus false. Note that bias or b is currently the most used notation for thresholds in neural networks.

We will create a sample perceptron model that distinguishes whether a dish is cooked good or bad to demonstrate all these theories. Let’s call this model – the Gordon Ramsay.

Figure 3: Perceptron Example

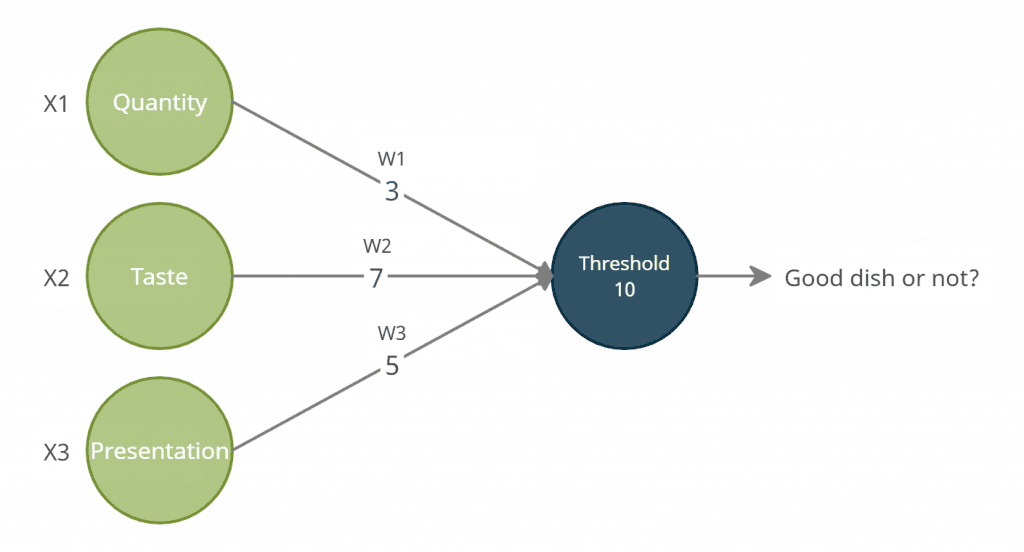
Gordon Ramsay has three input criteria: quantity, taste, and presentation. If there are too few or too much of the dish, the quantity criterion returns to zero. Similarly, the other criteria return to zero if the taste or the presentation is bad.

QuantityTastePresentationWeighted SumThresholdGood or Bad?
Few (0)Good (1)Good (1)3*0 + 7*1 + 5*1 = 1210Good
Enough (1)Good (1)Good (1)3*1 + 7*1 + 5*1 = 1510Good
Too Much (0)Bad (0)Good (1)3*0 + 7*0 + 5*1 = 510Bad
Table 1: Perceptron Example

To get the weighted sum, Ramsay adds all the products of each criterion’s weights and inputs. Then, it checks if the weighted sum exceeds the threshold constant. If it does, the dish is good. If it is doesn’t, the dish is bad.

But, what if the input values are not binary? This is where other activation functions come in.

Introduction to Activation Functions

Activation functions (aka Transfer Functions) decide whether a perceptron will “activate” or not. It also normalizes the output to a range between 1 and 0 or between -1 and 1. In our earlier example, we used an activation function called a binary step function to represent the standard equation of a basic perceptron.

Figure 4: Step Function

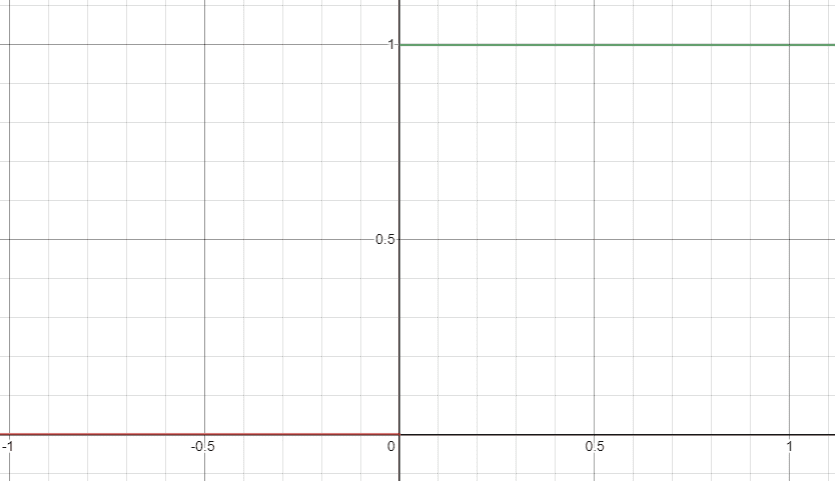
The problem with the step function is that it only allows two outputs: 1 and 0. An input barely above the threshold will have the same value of 1 as an input 10,000 times greater than the threshold. High sensitivity can be problematic in learning the weights and bias parameters as even minor changes in the parameters completely flip out the output.

To remedy this, we can use another activation function like sigmoid. Unlike the step function, the sigmoid function has an S-shaped curve bound between 0 and 1 (see Figure 5). This makes the gradient smoother, allowing floating outputs for precision.

Figure 5: Sigmoid Function

There are more activation functions in neural networks and deep learning. Each has its own advantages and disadvantages. You will understand them further as we proceed with the series. What’s important is you’re gaining intuition on how a single artificial neuron in a neural network works.

That said, we will now create a Python Perceptron.

Creating a Perceptron Model in Python

For starters, choose a code editor. I recommend using an interactive shell so you can see the output immediately after entering the code. This way, you can check every variable and output before you perform time-consuming tasks such as training.

Here, I prefer Jupyter Notebook. It’s a combination of a traditional editor and an interactive shell. You can use it to code, see the results, and save. You can even use it as a data visualization tool.

from sklearn.datasets import load_iris
iris = load_iris()
x = iris.data[:,(2,3)]

First, import your dataset from Scikit-learn. Scikit-learn is an open-source machine learning library. It provides various tools for model fitting, data preprocessing, model selection and evaluation, and many other utilities.

Scikit has a package called sklearn.datasets that contains sample datasets for quick testing. Inside this package is the Iris dataset. This data set contains three classes of 50 instances each, where each class refers to a type of the Iris plant: Iris-Setosa, Iris-Versicolour, and Iris-Virginica. Each instance contains four attributes: sepal length, sepal width, petal length, and petal width.

We will train our model using only petal length and petal width. Moreover, since a perceptron is limited to binary output, our perceptron will only detect whether the Iris plant is an Iris-Setosa or not.

Figure 6: Petal Width and Length

You can see the contents of x in Figure 6. We sliced the array containing the four attributes to obtain the petal width and length details only.

iris.target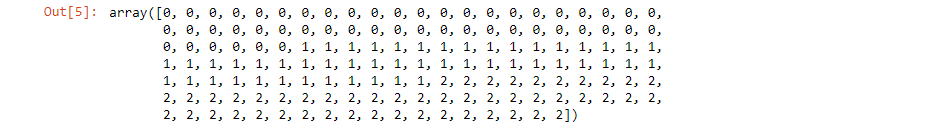
Figure 7: Target Values

By entering iris.target, you will see the list of all 150 instances of Iris plants labeled with the target values: 0 as Iris-Setosa, 1 as Iris-Versicolour, and 2 as Iris-Virginica (see Figure 7).

y = (iris.target == 0)
Figure 8: Boolean Labels

We want the 0-labeled instances since our goal is to detect the Iris-Setosa plant (see Figure 8).

y = (iris.target == 0).astype(int)
Figure 9: Integer Labels

Furthermore, we convert the Boolean information into binary integers (see Figure 9).

Now that we have both x and y values, we can now train the perceptron. Import Perceptron from the sklearn.linear_model package.

from sklearn.linear_model import Perceptron

Initialize the weight and bias parameters with random values, then fit the 150 pairs of petal width and length instances to y. This will update the parameters so that the perceptron distinguishes the Iris Setosa among the 150 instances. 

per_clf = Perceptron(random_state=42)
per_clf.fit(x,y)

Finally, use predict to check if the model works. Enter two floating values as hypothetical petal width and length. I used the first value from Figure 6 to confirm the validity of the model. Then, a wise guess for the second value.

ypredict = per_clf.predict([[1.4,0.2],[1.37,0.29]])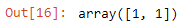

Remember!

  • A biological neuron only activates if the total input signal exceeds a certain threshold.
  • A perceptron is an artificial neuron. It is also a single-layer neural network.
  • Activation functions decide whether a perceptron will trigger or not.

That’s it for Perceptrons! See you next time as we move on to Neural Networks in Python: ANN. Feel free to leave a comment below if you have any questions.